Asset Returns

several definitions

Let P_t be the price of an asset at t, the one-period simple return is defined as:
R_t = (P_t−P_t-1)/P_t-1

and the one-period gross return is P_t/P_t-1 = R_t+1.

The holding period for an investment may be more than one unit. For any integer k ≥ 1, the k-period simple return is：

R_t(k) = (P_t−P_t-k)/P_t-k

and the k-period gross return is P_t/P_k-1 = R_t(k)+1

Returns are scale-free, meaning that they do not depend on the numeraire, they depend on how a unit of time is measured. So there are Daily returns, Weekly returns, Monthly returns etc.

The one-period log return is defined as:

r_t = logP_t−logP_t-1= log(P_t/P_t-1) = log(1 + Rt)

The k-period log return is:

r_t (k)= r_t +r_t-1 +...+r_t-k+1 

In many cases and applications, for the sake of convenience, we often use excess return

r_t-r^*_t , where r^*_t is a reference rate. We should bare in mind that risk-free rate and market return are two commonly used reference rate.

Tools

Time series

Time series consists of a set of observations measured over time, stationarity is an important concept in it, which means the statistical characteristics of a time series do not change over time.

To be strict stationary, the k-dimensional joint distribution of (X₁ ,...,X_K) should be the same as that of (X_t+1 ,...,X_t+k), for any positive integer k and any t.

To be covariance stationary, {X_t} should have a finite second moment ,meanwhile, both E(X_t) and Cov(X_t,,X_t+k), for any integer k, do not depend on t.

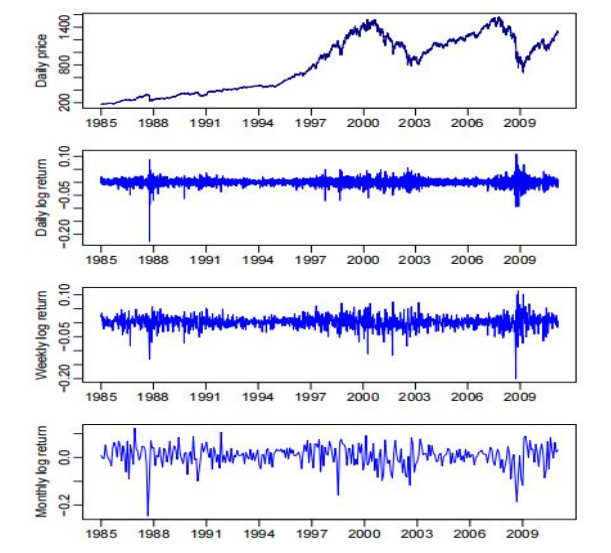
We can tell:

Asset prices are often not stationary over time, while most return sequences show certain level of stationary.

Volatility clustering(large price changes often occur in clusters)

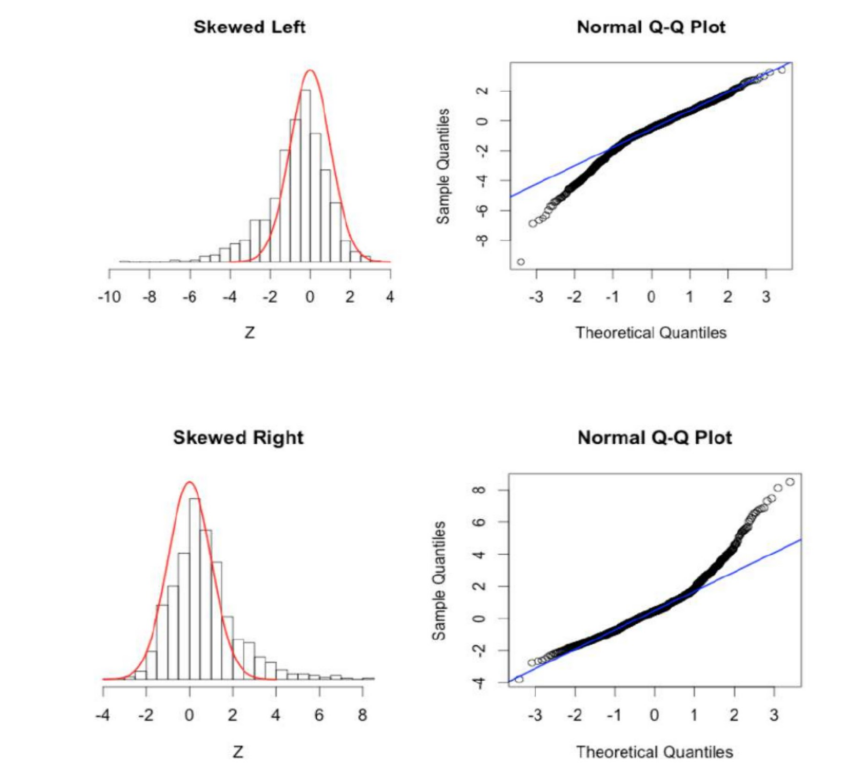
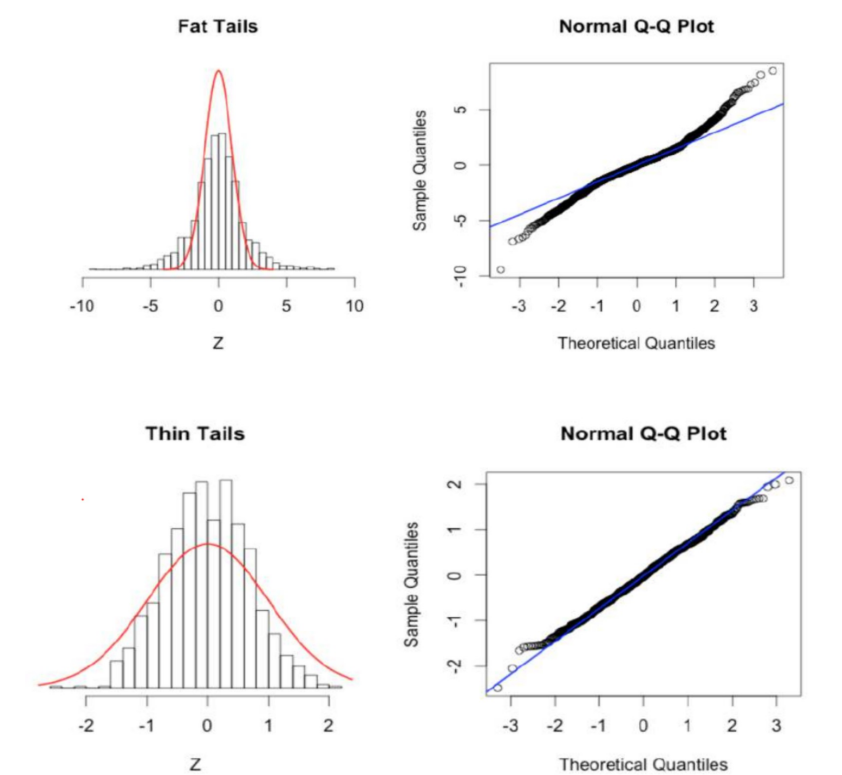
Q-Q Plot